Supervised Machine Learning Mastery
Analyze labeled data and implement supervised ML algorithms using Python for accurate predictions and pattern recognition.
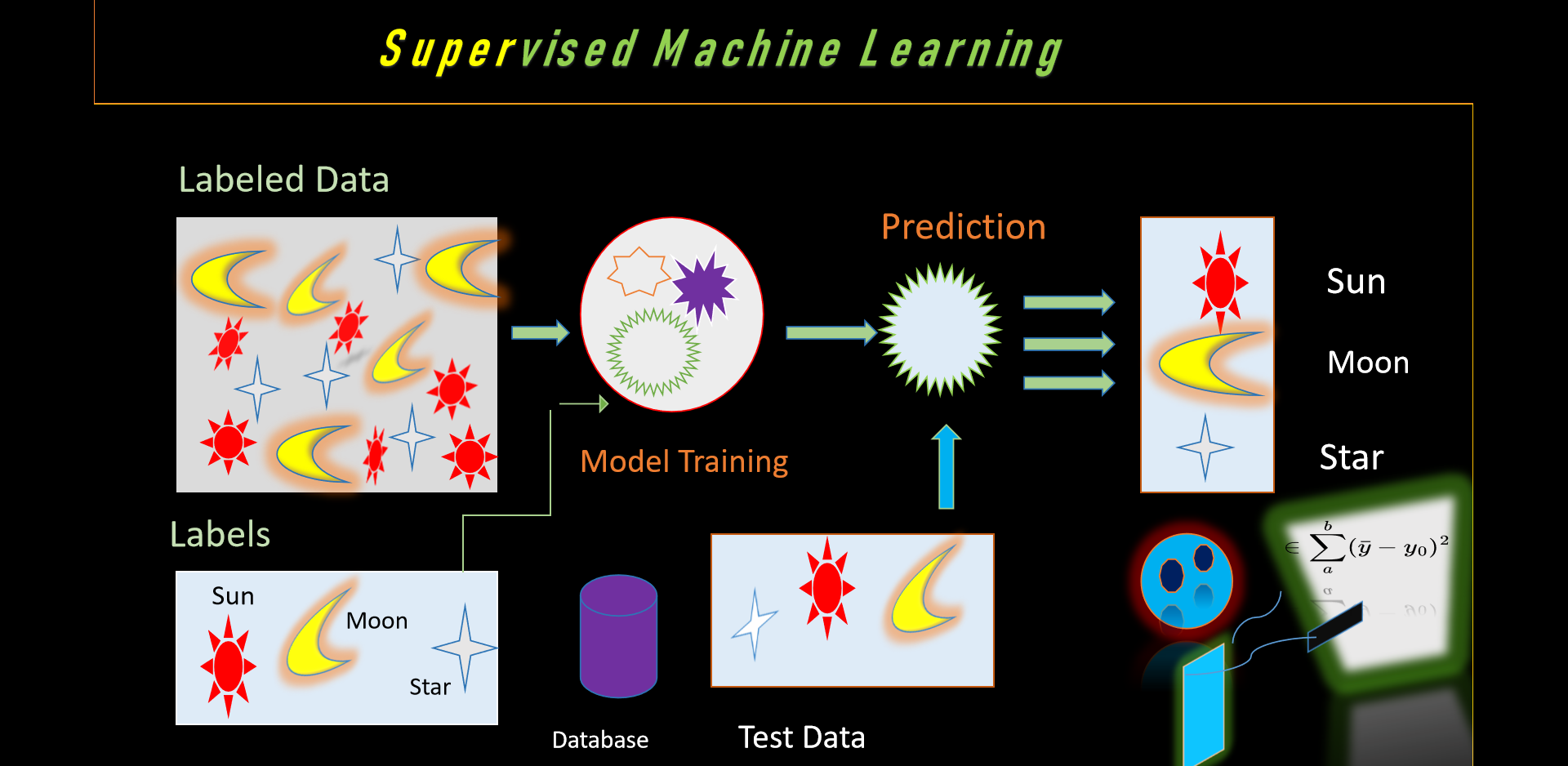
📈 Fig: Supervised
Machine Learning Pipeline
Core Algorithms
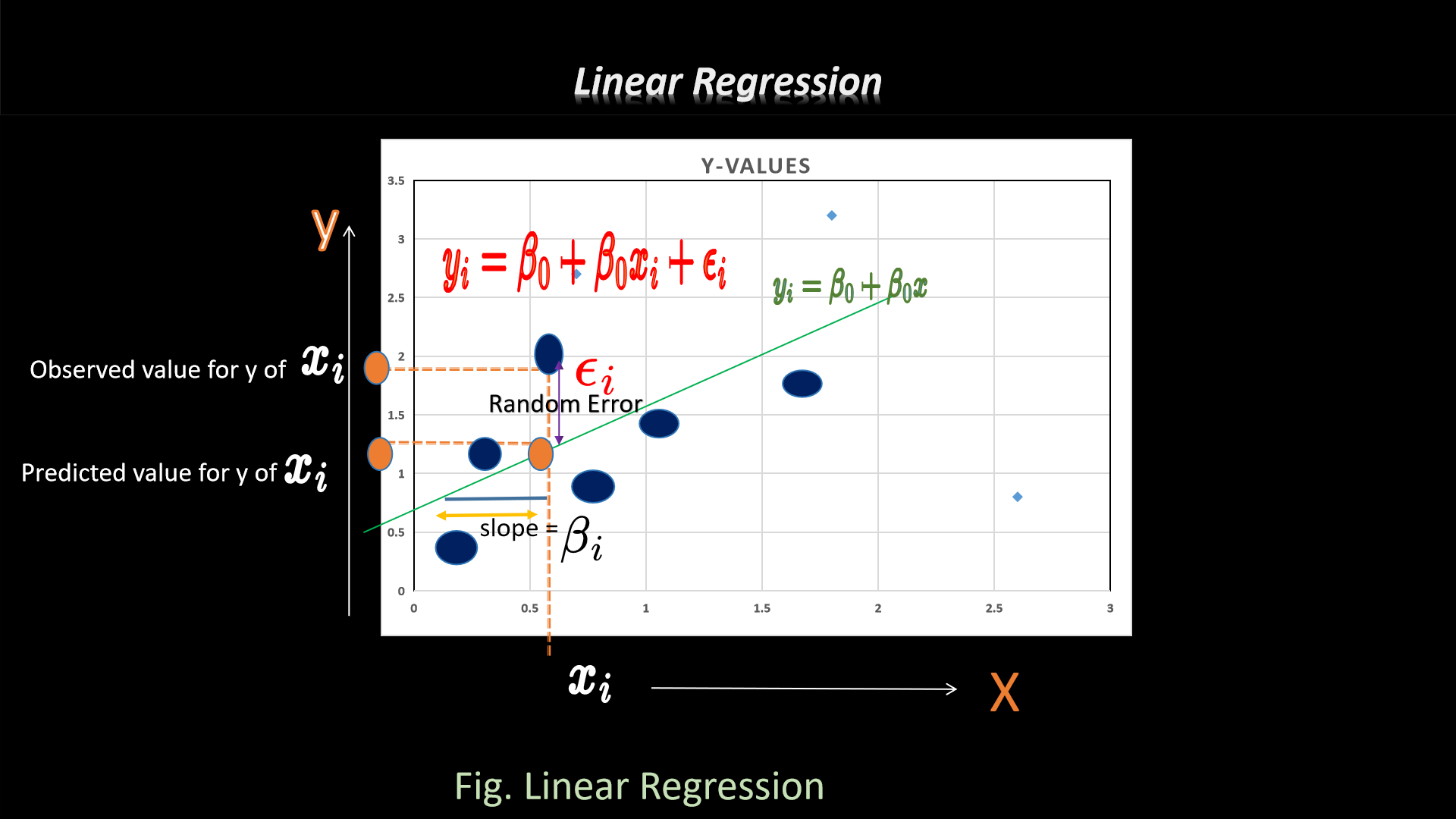
1. Linear Regression
Linear regression predicts continuous outcomes using the relationship y = β₀ + β₁x + ε.
Perfect for sales forecasting and trend analysis.[file:30]
🚀 Live Housing Price Prediction Demo
# Housing Price Prediction Pipeline
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import StandardScaler, OneHotEncoder
from sklearn.compose import ColumnTransformer
from sklearn.pipeline import Pipeline
from sklearn.metrics import mean_squared_error
# Load & preprocess data
data = pd.read_csv('Housing.csv')
num_attrs = ['area', 'bedrooms', 'bathrooms', 'stories', 'parking']
cat_attrs = ['mainroad', 'guestroom', 'basement', 'hotwaterheating',
'airconditioning', 'prefarea', 'furnishingstatus']
# Pipeline setup
num_pipeline = Pipeline([('scaler', StandardScaler())])
cat_pipeline = Pipeline([('encoder', OneHotEncoder())])
preprocessor = ColumnTransformer([
('num', num_pipeline, num_attrs),
('cat', cat_pipeline, cat_attrs)
])
X = preprocessor.fit_transform(data.drop('price', axis=1))
y = data['price']
# Train Linear Regression
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
lr = LinearRegression().fit(X_train, y_train)
preds = lr.predict(X_test)
rmse = np.sqrt(mean_squared_error(y_test, preds))
print(f"🏠 RMSE: ${rmse:,.0f}")
✅ Best Model: Linear Regression (RMSE: $889K) vs Random Forest
($968K)
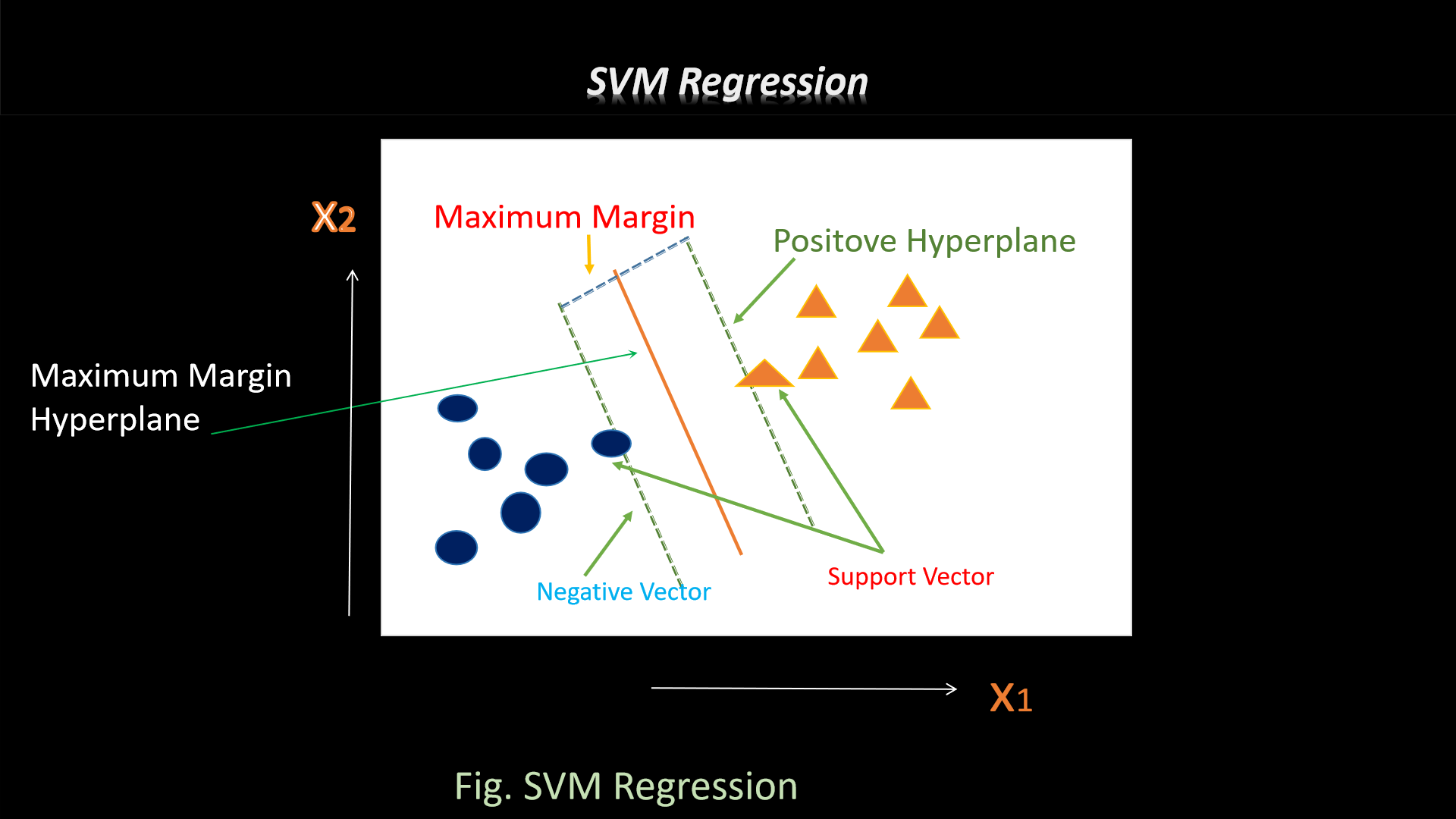
2. Support Vector Machines (SVM)
Hyperplane separation with maximum margin: wᵀx + b = 0. Excellent for high-dimensional
data.[file:30]
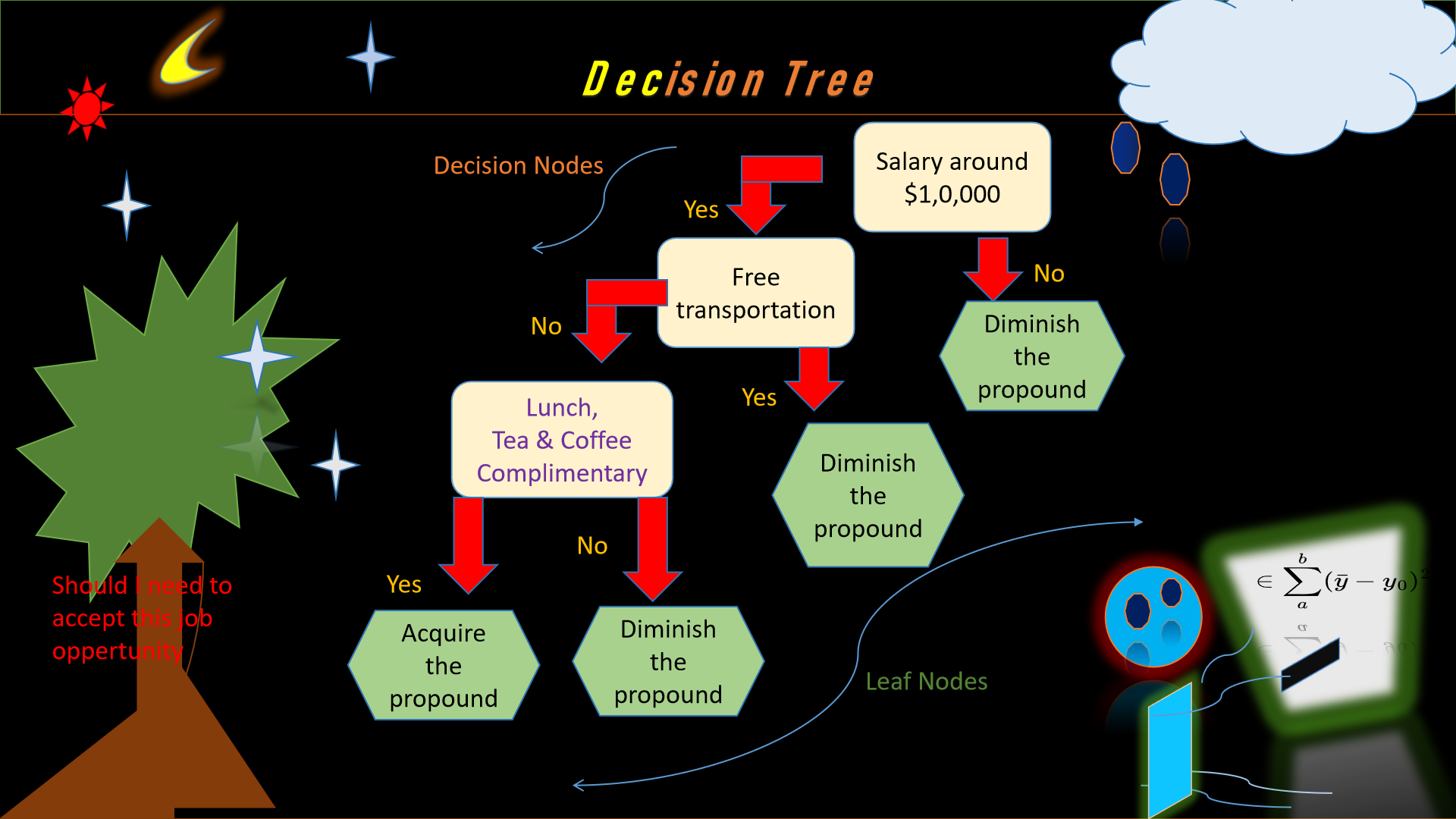
3. Decision Trees & Random Forest
🏆 Model Performance Comparison
| Model | Validation RMSE | Test RMSE |
|---|---|---|
| Linear Regression | $1.04M | $889K |
| Random Forest | $1.05M | $968K |
| Decision Tree | $1.72M | $1.64M |
| SVR | $2.00M | $1.75M |
Real-World Applications
- 📧 Spam Detection & Email Classification
- 🏥 Disease Prediction & Medical Diagnosis
- 💳 Fraud Detection & Credit Risk
- 📊 Stock Price Forecasting
💜 Supervised ML Playground
# 🏠 Paste Housing Price Prediction Code Here!
# Copy from the Linear Regression demo above 👆
import numpy as np
print("💜 AI Legend Supervised ML Playground")
print("Testing Linear Regression, Random Forest, SVM...")
print("Paste your model code and hit Run!")
# Quick test
prices = np.random.normal(500000, 200000, 10)
print("Sample prices:", prices[:3])
print("Ready for ML experiments! ✨")